Herons Method to Find Square Root of a Number
Heron's method is a simple algorithm to find the square root of any number. It starts by guessing the square root to be mean of 1 and the number itself. This guess becomes an upper limit of the approximation while the number divided by the guess becomes the lower limit. These two limits are compared and if they match within desired number of decimal places, we stop and the guess is reported as the answer.
Problem: Find the square root of a number.
Input: A positive number N and number of decimal places P for how close the answer should be.
Output: Square root of the number.
Algorithm Flowchart
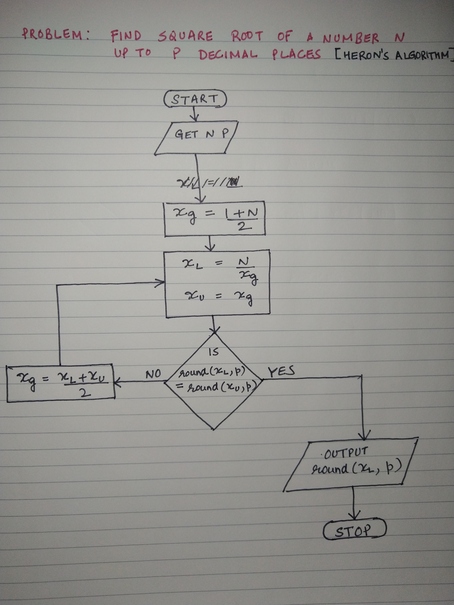
Implementation in Python
def squareroot(n, p):
"""function to compute squareroot using heron's algorithm
n is the number to calculate the squareroot of,
p is decimal points of precision"""
xg = (1 + n)/2
for i in range(1000):
xl = n / xg
xu = xg
if round(xl, p) == round(xu, p):
break
xg = (xl + xu) / 2
return(round(xl, p))
Is it correct?
To check correctness, I will compare it with built-in math.sqrt() function. Note
that the default relative tolerance of isclose() is 1e-09, so I set the
precision of squareroot() to 10:
from math import sqrt
from math import isclose
nums = [2, 23, 165, 1867, 16498]
for n in nums:
print(isclose(sqrt(n), squareroot(n, 10)))
In [56]: for n in nums:
...: print(isclose(sqrt(n), squareroot(n, 10)))
...:
True
True
True
True
True
In [57]:
Ok, the algorithm works correctly with our few test cases. I am curious now to find how fast (or slow!) it is compared to the built-in function.