Finding the Greatest Common Divisor
It turns out that the problem of finding the greatest common divisor can be hiding behind the problem we are solving. For example, let's imagine that there are 66 notebooks and 88 pencils that need to be distributed among a group of students. Problem is to find the maximum number of students such that each student gets the same number of pencils and notebooks while not leaving any stationary item on the table. This boils down to finding the greatest common divisor of 66 and 88. Similarly, if there are M computers, N printers and you are tasked to group these to form clusters containing m computers and n printers each, how many clusters can be formed such that none of the resources gets wasted?
Problem: Find the greatest common divisor.
Input: Two integers.
Output: An integer that is the GCD of the two input integers.
Algorithm Flowchart
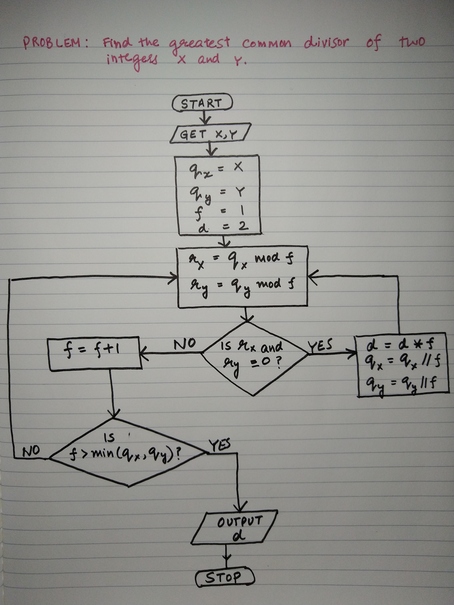
Implementation in Python
def gcd(x, y):
"""find the greatest common divisor of two integers x and y
"""
qx = x
qy = y
f = 2
d = 1
while f <= min(qx, qy):
rx = qx % f
ry = qy % f
if (rx == 0 and ry == 0):
d *= f
qx = qx // f
qy = qy // f
else:
f += 1
return(d)
Is it Correct?
Let's spotcheck our algorithm by comparing it with gcd() function from math
module:
In [11]: nums = [(42, 48), (48, 96), (1024, 4096), (3254, 4242)]
In [12]: for i in nums:
...: print(gcd(i[0], i[1]) == math.gcd(i[0], i[1]))
...:
True
True
True
True
In [13]:
Looks like it's working!. But once again comparing the performance of the two algorithms will be interesting.